Calculating $\pi$

In the figure below the square has the same diameter as the inscribed circle ($d = 2 r $). Rewriting the area of the circle in terms of the diameter $d$ we get:

$$ A_{circle} = \pi \left( \frac{d}{2} \right)^2 = \frac{\pi d^2}{4} \qquad _{...(2)}$$

The area of the square is $d^2$. Therefore $\pi$ can be calculate by the following expression

$$\pi = 4 . \frac{A_{circle}}{A_{square}} \qquad _{...(3)}$$

A statistical method can be used to determine the ratio of the area of the circle to the square. A number of random points are counted inside the square. The probability of random points found inside the circle is proportional to the area of the circle relative to the square.

The algorithm can be described as follows. Let N denote the total number of random points.

• Generate a random point inside the square with coordinates $(x_i, y_i)$. $x_i$ and $y_i$ are independent random numbers in the range -r to r
• Calculate the distance of the point from the origin. $\sqrt{x_i^2+y_i^2}$
• Count the number of points inside the circle. In the diagram below $(x_1, y_1)$ is inside the circle and $(x_2, y_2)$ is outside the circle
  • Inside the circle: $\sqrt{x_1^2+y_1^2} \le r$
  • Outside the circle: $\sqrt{x_2^2+y_2^2} \gt r$
• The estimate for $\pi$ is 4 x ( number of points inside the circle / N )

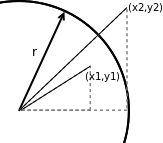
In the 2nd figure (to the right) 78 random points located inside the circle compare to a total of 100. Using the equation (3) we get:

$$\pi_{(N=100)} \approx 4 \times \frac{78}{100} = 3.12 $$

The accuracy can be improved by increasing the number of random points (e.g. 1000,  and 10000 points). 

For N = 1000, number of points inside the circle = 783

$$\pi_{(N=1000)} \approx 4 \times \frac{783}{1000} = 3.132 $$

The experiment can be repeated a number of times to get a mean value with an error estimate. The table below consists of 5 measurements for a sample of N random points.

There are 10 times as many random points in the trial for each subsequent row.

Sample size (points)	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Mean ($\mu$)	$\sigma$
100	3.16000	3.04000	3.28000	3.28000	3.28000	3.208000	0.107331
1000	3.07200	3.14400	3.22400	3.16800	3.23200	3.168000	0.065238
10,000	3.14800	3.12600	3.17720	3.12400	3.14040	3.143120	0.021514
100,000	3.13752	3.14116	3.13988	3.13392	3.14536	3.139568	0.004251
1,000,000	3.14412	3.14187	3.14189	3.14191	3.13887	3.141734	0.001869
107	3.14203	3.14099	3.14102	3.14221	3.14213	3.141677	0.000613
108	3.14172	3.14181	3.14163	3.14189	3.14159	3.141728	0.000124
109	3.14153	3.14165	3.14169	3.14167	3.14166	3.141640	0.000063
1010	3.14161	3.14158	3.14159	3.14158	3.14161	3.141593	0.000015
1011	3.14159	3.14159	3.14161	3.14159	3.14160	3.141594	0.000009

One can determine the value of $\pi$ by summing an series of terms as shown in equation (4) below

$$ \frac{\pi}{4} = \sum_{n=0}^\infty \frac{(-1)^n}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \frac{1}{13} - \frac{1}{15} + ... \qquad _{...(4)} $$

The formula is easy to remember. The denominator of each term is a sequence of odd numbers and the sign alternates for each successive term. A major drawback of this method is that the sum converges very slowly. The table below indicates that a large number of terms are required to obtain an high precision estimate of $\pi$. After adding 10 million terms, the estimate is accurate to 7 decimal places.

Number of terms	Sum
100	3.13159290
1000	3.14059265
10,000	3.14149265
100,000	3.14158265
1,000,000	3.14159165
10,000,000	3.14159255

Machin's formula for $\pi$

---

Despite the simplicity of the Leibniz formula it has been demonstrated in the previous section that the convergence rate is very slow. After summing 10 million terms, an accuracy of only 7 decimal places is achieved.

In 1706 John Machin found the following:

$$\frac{\pi}{4} = 4 \times \arctan(\frac{1}{5}) - \arctan(\frac{1}{239}) \qquad_{...(5)}$$

To determine $\arctan(x)$ the following series can be used for $-1 <= x <= 1$:

$$\arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} ...  \qquad_{...(6)}$$

For x = 1, the Leibniz formula for $\pi/4$ is obtained. However for small values of x the series will converge rapidly. A small number of terms are required to obtain a high precision estimate.

The table below shows the evaluation of the terms in equation (5)

Term	arctan(1/5)	sum	artan(1/239)	sum
1st	0.200000000000	0.200000000000	0.004184100418	0.004184100418
2nd	-0.002666666667	0.197333333333	-0.000000024417	0.004184076002
3rd	0.000064000000	0.197397333333	-	-
4th	-0.000001828571	0.197395504762	-	-
5th	0.000000056889	0.197395561651	-	-
6th	-0.000000001862	0.197395559789	-	-
7th	0.000000000063	0.197395559852	-	-
8th	-0.000000000002	0.197395559850	-	-

Summing 8 terms for $\arctan(\frac{1}{5})$ we get 0.197395559850. Only 2 terms for $\arctan(\frac{1}{239})$ are required to obtain 0.004184076002.

Substituting the evaluated sums into equation (5) we get:

4 x ( 4 x 0.197395559850 - 0.004184076002) = 3.14159265359

High Precision calculation

One can determine the value of $\pi$ using fixed point arithmetic (instead of floating point). Using this method the number one is represented as a very large number (i.e. 10¹⁰⁰). An arithmetic operation such as a multiplication or division performed on a very large number will result in a high precision calculation. Take the following example:

1 / 997 =  0.001003009027 (to 12 decimal places).

Representing 1 as 1 x 10¹⁰⁰:

1 x 10¹⁰⁰ / 997 = 10030090270812437311935807422266800401203610832497492477432296890672016048144433299899699097291875

The first 10 digits match the floating point calculation. However an additional 90 digits have been determined not possible using conventional floating point arithmetic. Once the operation is complete we simply move the decimal place to the left into the correct position. This simple trick is applied to the evaluation of the terms in the series.

To avoid floating point arithmetic we can re-write equation (5) as:

$$\frac{\pi}{4} = 4 \times arccot(5) - arccot(239) \qquad_{...(7)}$$

Substituting $u=1/x$ into equation (6) we get:

$$arccot(u) = \frac{1}{u} - \frac{1}{3u^3} + \frac{1}{5u^5} - \frac{1}{7u^7} + ... \qquad_{...(8)}$$

The problem has been reduced to the following steps:

• Evaluate arccot(5) and arccot(239) using equation (8) with fixed point arithmetic
• For fixed point arithmetic operations:
  • Represent 1 as a large number, depending on how many decimal places are required, e.g. for 1000 decimal places, 1 is represented as 1 x 10¹⁰⁰⁰
  • Continue to evaluate terms until the term itself is equal to zero
  • To avoid rounding errors, additional guard digits are used.⁽⁴⁾
• Substitute arccot(5) and arccot(239) into equation (7) to get a final determination of $\pi$.

Python is a suitable high level scripting language that runs on most computing platforms and can perform high precision arithmetic using long integers. Combining the basic concepts from two python scripts (references (5) and (6)) equation (7) can be evaluated to a high precision.

The number of decimal places can be easily set in the main loop of the script.

Executing the python script we get $\pi$ to 1000 decimal places:

... calculating pi to 1000 decimal places
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989 

Conclusion

Three relatively simple methods to determine the value of $\pi$ have been described and demonstrated in this article.

The Monte Carlo simulation uses random points to estimate the area of a square and an inscribed circle inside the square. Accurately determining the ratio of the areas of two geometric closed objects using random points is inefficient. Counting one million random points provides an estimate that is no more accurate than 2 decimal places. Taking the average of 5 trials with 100 billion random points results in a value accurate to 6 decimal places, allowing for the uncertainty in the average.

The Leibniz formula offers an easy way to compute $\pi$ but is also highly inefficient requiring the summation of 10 million terms to achieve an estimate accurate to 7 decimal places.

Machin's formula makes use of a trigonometric relationship containing $\arctan(x)$ which converges rapidly for small values of x. It forms the basis of more advanced methods for calculating $\pi$. One can overcome the limitations of floating point arithmetic and adopt fixed point arithmetic with long integers to estimate $\pi$ to many digits.

A summary of the results reported in this article is tabulated below:

Method	Estimate
Monte Carlo simulation (5 trials of 100 billion points)	3.141594 +/- 0.000009
Leibniz formula (sum of 10 million terms)	3.14159255
Machin's formula (floating point)	3.14159265359
Machin's formula (fixed point to 1000 decimal places)	3.141592653589793238...1989

More sophisticated methods exist for calculating $\pi$. For further reading also check out an excellent article on wikipedia which covers a detailed cronology of the computation of pi

References

---

1. Pi: http://en.wikipedia.org/wiki/Pi
2. Monte Carlo Pi: http://math.fullerton.edu/mathews/n2003/montecarlopimod.html
3. Calculating Pi with the Monte Carlo method: http://learntofish.wordpress.com/2010/10/13/calculating-pi-with-the-mont...
4. Pi - Machin: http://www.craig-wood.com/nick/articles/pi-machin/
5. Pi with Machin's formula: http://en.literateprograms.org/Pi_with_Machin's_formula_(Python)
6. Maclaurin Series: http://www.intmath.com/series-expansion/2-maclaurin-series.php

Appendix

---

Proofs

Leibniz formula for $\pi$

It can be shown from elementary trigonometry that $\tan (\pi / 4) = 1$. The inverse of this relationship is:

$$\frac{\pi}{4} = \tan^{-1} \left( 1 \right) = \arctan ( 1 )  \qquad_{...(1)} $$

Any continuous function can written as a series of polynomials near some value $x=a$ using the Taylor series. A special case of the Taylor series is $a=0$ which is known as the Maclaurin series⁽⁵⁾.

We can express $\arctan(x) = f(x)$ as an infinite sum of terms.

$$ f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f^{(3)}(0)}{3!}x^3 + ... + \frac{f^{n}(0)}{n!}x^n + ...  \qquad_{...(2)} $$

Evaluating the higher order derivatives using the quotient rule in calculus we get the following:

Derivatives	Values
$f(x) = \arctan(x)$	$f(0) = 0$
$f'(x) = \frac{1}{1+x^2}$	$f'(0) = 1$
$f''(x) = \frac{-2x}{(1+x^2)^2} $	$f''(0) = 0$
$f^{(3)} (x) = \frac{2(3x^2-1)}{(1+x^2)^3} $	$f^{(3)}(0) = -2 $
$f^{(4)}(x) = \frac{-24x(x^2-1)}{(1+x^2)^4}$	$f^{(4)}(0) = 0$
$f^{(5)}(x) = \frac{24(5x^4-10x^2+1)}{(1+x^2)^5} $	$f^{(5)}(0) = 24 $

If we now substitute the values into equation (2) we get the following:

$$\begin{align} \arctan(x) &= 0 + x + 0 + \frac{-2}{3.2.1}x^3 + 0 + \frac{+24}{5.4.3.2.1}x^5 + ...  \\ &= x - \frac{x^3}{3} + \frac{x^5}{5} - ... \end{align}  \qquad_{...(3)}$$

Therefore,

$$\arctan(1) = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + ... $$

Scripts

Monte Carlo simulation

The following script was used for the Monte Carlo simulation. The number of random points can be set with the variable N in the main section.

Notes:

• The number of random points, N, has been set to 1,000,000 in the main section of the script. This can be changed to whatever value is required. Obviously the larger the value of N, the longer the time required to reach a final value.
• In the simulation random points are selected inside a square of length 2 units. The inscribed circle has a radius of one unit.
• The simulation uses a whole circle even though a quadrant would have been more efficient.

#!/usr/bin/python
#
# Monte Carlo simulation to determine pi
#
# John Giovannis - Dec 2011
#
import math
import sys
from random import random

# ---------------------------------------------------
 
def hypot(x,y):
    a = math.sqrt(x*x + y*y)
    return a
 
# ---------------------------------------------------
 
def calc_pi(max):
 
    n = 0
    inside = 0
 
    # loop until the value "max" is reached
    while (n < max):
        n += 1
        
        # pick a random point inside a box
        x = 2*random() - 1
        y = 2*random() - 1
 
        # calculate the distance of the point from the centre
        h = hypot(x, y)
     
     	# determine if the point is inside the circle
        if h <= 1.0:
            inside += 1
 
    # calculate pi based on the number of points inside the circle
    pi = 4 * ( inside / float(n) )
 
    print "# points inside circle = %10d " % inside
    print "# points inside square = %10d " % n
 
    return pi
 
# ---------------------------------------------------
 
def main():
 
    # number of random points to count
    N = 1000000
    np = long(N)
 
    print "Monte Carlo simulation in progress"
    pi_estimate = calc_pi(np)
     
    print "pi (estimate)          = %10.6f " % pi_estimate
    sys.stdout.flush()
 
 
 
# ===================================================
# Main
 
if __name__ == '__main__':
    main()

#!/usr/bin/python
#
# Calculate pi to many decimal places using long arithmetic
# .. based on python listing in
#    http://en.literateprograms.org/Pi_with_Machin's_formula_(Python)
#
# John Giovannis - Dec 2011
#
# ---------------------------------------------------
 
def arccot(u):
# calculate arccot of an integer using long arthimetic

		# initialise the sum and first term
        sum = num = one // u

		# pre-calculate u^2
        u2 = u*u

		# initialise denominator
        den = 3

        while 1:
				# evaluate the next numerator in the series
                num = - num // u2

				# evaluate the term
                term = num // den

				# break out of the loop if the term is equal to zero
                if term == 0:
                        break

				# update the denominator
                den += 2

				# update the sum in the series
                sum += term
 
        return sum

# --------------------------------------------------- 
 
def calc_pi(ndp):
        global one
		# represent the number 1 (as a large number)
        one = 10**(ndp+10)
 
        print "... calculating pi to %d decimal places" % ndp

		# evaluate pi
        pi = 4 * (4 * arccot(5) - arccot(239))

		# ... final division to allow for the guard digits
        pi = pi // (10**10)
 
        print "%s \n" % pi

# ---------------------------------------------------
 
def main():
		# calculate pi to 1000 decimal places
        calc_pi(1000000)
 
 
# ===================================================
# Main
 
if __name__ == '__main__':
        main()